Strong Convexity and Its Generalization
Introduction
The convex condition of the objective function guarantees extrema uniqueness. It says that if \(f\) is convex, we can discuss the convergence rate of optimization methods by estimating \(||f(w_t)-f^{opt}||\), where \(f^{opt}\) is the global maximum/minimum (optimum). Otherwise, we know nothing about the distance and only discuss \(\min_{t\in\{0,1,\dots,T\}}||\nabla f(w^t)||^{2}\).
Intuitively, the convexity requires that the function graph is above its tangent line. A typical example is a quadratic function: \(f(x) = ax^2+bx+c\). If \(a>0\), it is convex. One can validate this observation by sketch its tangent line.
However, there are lots of "flat" convex functions. Their graphs are above the corresponding tangent lines, but they are very close. The following figure draws a convex and flat basin:
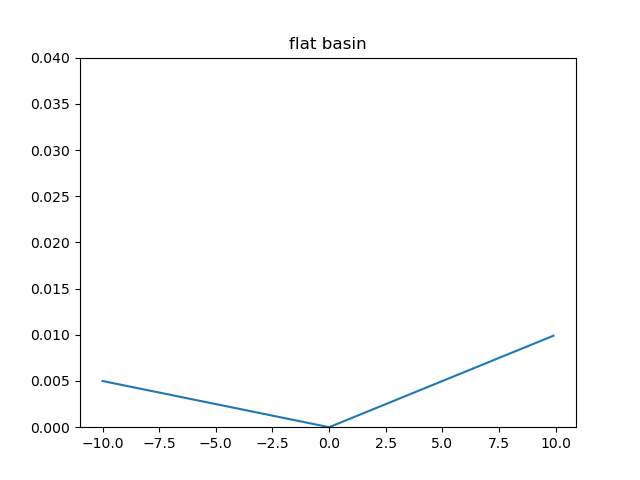
We can find that the graph coincides with its tangent line. The problem is that these functions provide low gradients, which lead to a sub-linear convergence rate of the gradient descent method. We hope to avoid discussing these cases; the strong convexity constrains the functions by requesting them to own a quadratic lower bound. The optimization is much more comfortable in the strong convex cases, and a global linear convergence rate can be achieved.
The strong convexity is a strong assumption, and we want to discuss its generalization in this work.
Relation Between Conditions
Strong convexity is a strong assumption to guarantee the linear convergence rate in our discussion. We formulate it as follows:
Strong Convexity(SC): For all \(x\) and \(y\) we have \[ f(y)\ge f(x)+\nabla f(x)^T(y-x)+\frac{\mu}{2}||y-x||^2 \] Suppose you are curious about how to prove gradient descent (GD) and stochastic gradient descent (SGD) have linear convergence rate under strong convexity assumption. In that case, you can find them in this work: Convergence Theorems for Gradient Descent.
We only concern about SC's generalizations and theirs relation.
Essential Strong Convexity(ESC): For all \(x\) and \(y\) such that \(x_p=y_p\), we have \[ f(y)\ge f(x)+\nabla f(x)^T(y-x)+\frac{\mu}{2}||y-x||^2 \] Where \(x_p\) is the projection of \(x\) onto the solution set \(\mathcal{X}^{opt}\).
Obviously, ESC is weaker than SC: \(SC\Rightarrow ESC\).
Weak Strong Convexity(WSC): For all \(x\) we have \[ f^*\ge f(x)+\nabla f(x)^T(x_p-x)+\frac{\mu}{2}||x_p-x||^2 \] Let \(y=x_p\), then we can prove that \(ESC\Rightarrow WSC\).
Restricted Secant Inequality(RSI): For all \(x\) we have \[ \nabla f(x)^T(x-x_p)\ge\mu||x_p-x||^2 \] If we further assume function \(f\) is convex, then the condition is called Restricted Strong Convexity(RSC).
Re-order the WSC inequality: \[ \nabla f(x)^T(x-x_p)\ge f(x)-f^{opt}+\frac{\mu}{2}||x_p-x||^2 \] Because \(f^{*}\) is the lower bound of \(f(x)\), \(f(x)-f^{opt}\ge0\).
Therefore, \(WSC\Rightarrow RSI\).
Error Bound(EB): For all \(x\) we have \[ ||\nabla f(x)||\ge\mu(x_p-x) \] Since \(||\nabla f(x)||||x-x_p||\ge\nabla f(x)^T(x-x_p)\), dividing both side of RSI by \(||x-x_p||\) we can prove \(RSI\Rightarrow EB\).
Polyak-Lojasiewicz(PL): For all x we have \[ \frac{1}{2}||\nabla f(x)||^2\ge\mu(f(x)-f^{opt}) \] PL inequality is commonly used in recent researches. This assumption is more general than Strong convexity and sufficient to guarantee linear convergence. Furthermore, we can prove that it is equivalent to the EB assumption.(Assumption on Lipschitz continuity of gradients is necessary.)
We show that \(EB\Rightarrow PL\):
Lipschitz continuity is a strong assumption on function continuity. The \(L\)-Lipschitz continuity of \(g(x)\) is defined by the following inequality: \[ ||g(x)-g(y)||\le L||x-y||, \forall x,y\in \mathcal{D}_g \] If \(f(x)\) has \(L\)-Lipschitz continuous gradient, say, \(||\nabla f(x)-\nabla f(y)||\le L||x-y||\). Then \[ f(x)\le f(x_p)+\nabla f(x_p)^T(x-x_p)+\frac{L}{2}||x_p-x||^2 \] Let \(f(x_p)=f^*\), the corresponding gradients are equal to zero vector. We have \[ f(x)-f^{opt}\le\frac{L}{2}||x_p-x||^2 \] Applying EB, \[ f(x)-f^{opt}\le\frac{L}{2\mu}||\nabla f(x)||^2 \] For \(PL\Rightarrow EB\),
We firstly introduce another assumption weaker than PL.
Quadratic Growth(QG): For all \(x\) we have \[ f(x)-f^{opt}\ge\frac{\mu}{2}||x_p-x||^2 \] If we further assume \(f(x)\) is convex, this case is called optimal strong convexity.
We show that \(PL\Rightarrow QG\),
Define the following function: \[ g(x) = \sqrt{f(x)-f^{opt}} \] If \(f(\cdot)\) satisfies PL inequality, then for any \(x\notin \mathcal{X}^{opt}\): \[ ||\nabla g(x)||^2=\frac{||\nabla f(x)||^2}{f(x)-f^{opt}}\ge2\mu \] For any point \(x_0\notin\mathcal{X}^*\), consider solving the following differential equation: \[ \frac{d x(t)}{dt}=-\nabla g(x(t))\\ x(t=0)=x_0 \] The solution defines a flow orbit starting at \(x_0\) and flowing along the gradient of \(g(\cdot)\). \[ \begin{equation} \begin{aligned} g(x_0)-g(x_t)&=\int_{x_t}^{x_0}\nabla g(x)^Tdx\\ &=-\int_{x_0}^{x_t}\nabla g(x)^Tdx\\ &=-\int_{0}^{T}\nabla g(x(t))^T\frac{d x(t)}{dt}dt\\ &=\int_{0}^T||\nabla g(x(t))||^2dt\\ &\ge\int_{0}^T2\mu dt\\ &=2\mu T \end{aligned} \end{equation} \] Notice that \(g(x_t)\ge 0\), thus we know that \(T\le\frac{g(x_0)}{2\mu}\), so there must be a \(T\) with \(x(T)\in\mathcal{X}^{opt}\).
The length of the orbit can be calculated by the following integral, \[ \mathcal{L}(x_0)=\int_0^T||\frac{dx(t)}{dt}||dt=\int_0^T||\nabla g(x(t))||dt\ge||x_0-x_p|| \] \(x_p\) is the projection of \(x_0\) onto \(\mathcal{X}^{opt}\)
Recall that: \[ \begin{equation} \begin{aligned} g(x_0)-g(x_T)&=\int_0^T||\nabla g(x(t))||^2dt\\ &\ge\sqrt{2\mu}\int_{0}^T||\nabla g(x(t))||dt\\ &\ge\sqrt{2\mu}||x_0-x_p|| \end{aligned} \end{equation} \] Since \(g(x_T)=0\), according to the definition of \(g(\cdot)\): \[ f(x)-f^*\ge2\mu||x-x_p||^2 \] It is the QG inequality.
Now, we turn to the proof of \(PL\Rightarrow EB\),
Using the above result. We denote the PL constant as \(\mu_p\) and QG constant as \(\mu_q\), \[ \frac{1}{2}||\nabla f(x)||^2\ge\mu_p(f(x)-f^*)\ge\frac{\mu_p\mu_q}{2}||x-x_p||^2 \] Thus, we derive the EB inequality: \[ ||\nabla f(x)||\ge\sqrt{\mu_p\mu_q}||x-x_p|| \] what if we assume \(f(\cdot)\) is convex?
Actually, \(RSI\Leftrightarrow EB\Leftrightarrow PL\Leftrightarrow QG\) hold in this case.
We prove this observation by showing that \(QG+Convex\Rightarrow RSI\),
By convexity we have, \[ f(x_p)\ge f(x)+\nabla f(x)^T(x_p-x) \] Applying QG inequality, \[ \nabla f(x)^T(x-x_P)\ge f(x)-f^{opt}\ge\frac{\mu}{2}||x_p-x||^2 \] Which is RSI inequality.
Conclusion
In the end, we finish our work by a relation graph:
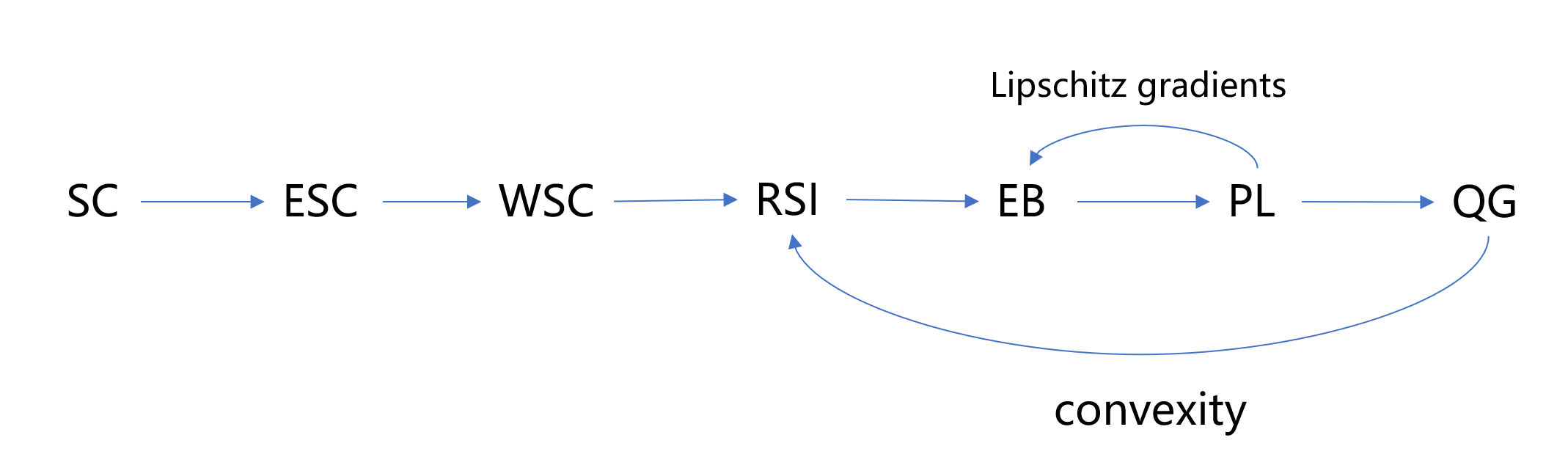
Most of the content comes from the following work: